ระบบตัวเลขที่รู้จักและใช้กันอยู่ในชีวิตประจำวัน คือ เลขฐานสิบ (Decimal Number) ในระบบดิจิตอลยังมีตัวเลขที่สำคัญที่ควรรู้จัก คือ เลขฐานสอง (Binary Number) เลขฐานแปด ( Octal Number) และเลขฐานสิบหก ( Hexadicimal Number) แสดงตัวเลขของระบบเลขฐานต่างๆ ดังตารางที่ 6.1
ตารางที่ 1 แสดงตัวเลขของเลขฐานสอง ฐานแปด ฐานสิบ และฐานสิบหก
| เลขฐาน | ตัวเลขพื้นฐาน |
| ฐานสอง ฐานแปด ฐานสิบ ฐานสิบหก | 0, 1 0, 1, 2, 3, 4, 5, 6, 7 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
ระบบเลขฐานสิบ เป็นระบบตัวเลขที่ใช้ในชีวิตประจำวัน ประกอบด้วยตัวเลข 10 ตัว คือ 0, 1, 2, 3, 4, 5, 6, 7, 8 และ 9
การนับเลขในระบบเลขฐานสิบ หลักหน่วยจะเริ่มจาก 0 ถึง 9 และเพิ่มเป็นสองหลัก โดยเพิ่มหลัก ซ้ายมือด้วยเลข 1 ดังตารางที่ 6.2
2 ระบบเลขฐานสอง
ระบบเลขฐานสอง เป็นระบบตัวเลขที่เหมาะสมกับการทำงานในระบบดิจิตอล และคอมพิวเตอร์ เลขฐานสองประกอบด้วยตัวเลข 2 ตัว คือ 0 และ 1 ซึ่งตัวเลขแต่ละตัวจะเรียกว่า บิต (bit) ซึ่งย่อมาจาก Binary Digit
การนับเลขในระบบเลขฐานสอง หลักหน่วยจะเริ่มจาก 0 ถึง 1 และเพิ่มขึ้นเป็น สองหลัก โดยเพิ่มหลักซ้ายมือด้วยเลข 1 ดังตารางที่ 2
ตารางที่ 2 ตารางแสดงการนับแบบเรียงลำดับของเลขฐานสอง, แปด, สิบ และสิบหก
| เลขฐานสอง (Binary) | เลขฐานแปด (Octal) | เลขฐานสิบ (Decimal) | เลขฐานสิบหก (Hexadecimal) |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
| 10000 | 20 | 16 | 10 |
3 ระบบเลขฐานแปด
ระบบเลขฐานแปด เป็นระบบตัวเลขที่มักใช้ในระบบคอมพิวเตอร์ ตัวเลขในระบบเลขฐานแปด ประกอบด้วยตัวเลข 8 ตัว คือ 0, 1, 2, 3, 4, 5, 6 และ 7
การนับเลขในระบบเลขฐานแปด หลักหน่วยจะเริ่มจาก 0 ถึง 7 และเพิ่มขึ้นเป็น สองหลัก โดยเพิ่มหลักซ้ายมือด้วยเลข 1 ดังตารางที่ 6.2
4 ระบบเลขฐานสิบหก
ระบบเลขฐานสิบหก เป็นระบบตัวเลขที่ใช้ในงานคอมพิวเตอร์ปัจจุบัน ประกอบด้วยตัวเลข 16 ตัว คือ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E และ F
การนับเลขในระบบเลขฐานสิบหก หลักหน่วยจะเริ่มจาก 0 ถึง F และเพิ่มขึ้นเป็น สองหลัก โดยเพิ่มหลักซ้ายมือด้วยเลข 1 ดังตารางที่ 6.2
5 การเปลี่ยนฐานของระบบตัวเลข (Converting Number System)
ในระบบตัวเลขที่ได้กล่าวมาแล้วข้างต้นสามารถเปลี่ยนฐานของระบบตัวเลขไปมาระหว่างกันได้ เช่น การเปลี่ยนเลขฐานสิบเป็นเลขฐานสอง การเปลี่ยนเลขฐานสองเป็นฐานสิบ หรือฐานแปด หรือฐานสิบหก เป็นต้น
5.1 การเปลี่ยนเลขฐานสองเป็นเลขฐานสิบ
การเปลี่ยนเลขฐานสองเป็นเลขฐานสิบ สามารถหาได้โดยใช้สูตรหรือโดยการคูณ แต่ละตัวเลข ของเลขฐานสองด้วยน้ำหนักที่ตำแหน่งนั้น แล้วนำผลที่ได้มารวมกันจากสูตร
N = dn Rn +…+ d3R3 + d2R2 + d1R1 + d0R0 N = … + 8d3 + 4d2 + 2d1 + 1d0
เมื่อ N = เลขฐานสิบ
R = ค่าเลขฐาน
d3, d2, d1, d0 มีค่าเป็น 0 หรือ 1
ดังนั้นการเปลี่ยนเลขฐานสองเป็นเลขฐานสิบ ทำได้โดย บวกค่าประจำตำแหน่งของแต่ละตำแหน่งตรงเลขฐานสองที่มีค่าเป็น 1 เท่านั้น
ตัวอย่างที่ 1 จงเปลี่ยนเลขฐานสองต่อไปนี้เป็นเลขฐานสิบ
ก) 10111 ข) 1101101
วิธีทำ
ก) (10111)2 = (1 24) + (0 23) + (1 22) + (1 21) + (1 20)
= 16 + 0 + 4 + 2 + 1
= (23)10
ข) (1101101)2 = (1 26) + (1 25) + (0 24) + (1 23) + (1 22) + (0 21) +(1 20)
= 64 + 32 + 0 + 8 + 4 + 0 + 1
= (109)10
ถ้าหากเลขฐานสองเป็นเลขทศนิยม สามารถเปลี่ยนเลขฐานสองเป็นเลขฐานสิบ ได้จากสูตร
N = d1R-1+ d2R-2 + d3R-3 + d4R-4 +….+ dnR-n
ตัวอย่างที่ 2 จงเปลี่ยนเลขฐานสองต่อไปนี้เป็นเลขฐานสิบ
ก) 0.101101
ข) 0.01101
วิธีทำ
ก) (0.101101)2 = (1 2-1) + (0 2-2) + (1 2-3) + (1 2-4) + (0 2-5) + (1 2-6)
= 0.5 + 0 + 0.125 + 0.0625 + 0 + 0.01525
= (0.703125)10
ข) (0.01101)2 = (0 2-1) + (1 2-2) + (1 2-3) + (0 2-4) + (1 2-5)
= 0 + 0.25+ 0.125 + 0 + 0.03125
= (0.40625)10
ตัวอย่างที่ 3 จงเปลี่ยนเลขฐานสอง 11101.0111 ให้เป็นเลขฐานสิบ
วิธีทำ
(11101.0111)2 = (1 24) + (1 23) + (1 22) + (0 21) + (120) +(0 2-1)
+(1 2-2) + (1 2-3) + (1 2-4)
= 16+8+4+0+1+0.25+0.125+0.0625
= (29.4375)10
การเปลี่ยนเลขฐานสองเป็นฐานสิบ ทั้งจำนวนเต็มและทศนิยมสามารถเขียนอยู่ในรูปของเลขยกกำลังของเลข 2 ของหลักนั้นๆ ดังตารางที่ 6.3
ตารางที่ 6.3 ตารางแสดงค่าเลขยกกำลังของเลข 2
| 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 2-1 | 2-2 | 2-3 | 2-4 | 2-5 |
| 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 0.5 | 0.25 | 0.125 | 0.0125 | 0.0312 |
ก) 1011.101
ข) 11010.1101
วิธีทำ
| 24 | 23 | 22 | 21 | 20 | 2-1 | 2-2 | 2-3 | 2-4 | เลขยกกำลังของเลข 2 |
| 16 | 8 | 4 | 2 | 1 | 0.5 | 0.25 | 0.125 | 0.0625 | ค่าของเลขฐานสิบ |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 8+2+1+0.5+0.125=11.625 | ||
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 16+8+2+0.5+0.25+0.0625= 26.8125 |
การเปลี่ยนเลขฐานสิบเป็นเลขฐานสอง ทำได้โดยการเอาเลขฐานสิบตั้งแล้วหารด้วย 2 เก็บเศษที่เหลือจากการหารไว้ (ซึ่งมีเพียงเลข 1 กับเลข 0 เท่านั้น) การหารให้หารไปจนกว่าผลลัพธ์จะเป็นเลข 0
การอ่านเลขฐานสองที่จะได้จากการหาร จะอ่านจากเศษตัวสุดท้ายเป็นหลักที่มีความสำคัญมากที่สุด (Most Significant Digit : MSD) และเศษตัวแรกเป็นหลักที่มีความสำคัญน้อยสุด (Least Significant Digit : LSD)
ตัวอย่างที่ 5 จงเปลี่ยน (24)10 เป็นเลขฐานสอง
วิธีทำ

ดังนั้้น …… (24)10 = (11000)2
เราสามารถตรวจเช็คคำตอบได้โดยการเปลี่ยนเลขฐานสองกลับมาเป็นเลขฐานสิบ
(11000)2 = (1 24) + (1 23) + (0 22) + (0 21) + (0 20)
= 16 + 8 + 0 + 0 + 0
= (24)10
ตัวอย่างที่ 6 จงเปลี่ยน (37)10 เป็นเลขฐานสอง
วิธีทำ

ดังนั้น …… (37)10 = (100101)2
ตัวอย่างที่ 7 จงเปลี่ยน (355)10 เป็นเลขฐานสอง วิธีทำ
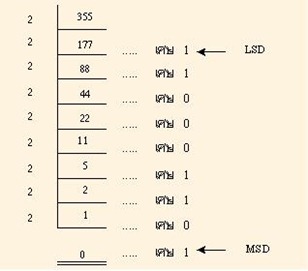
ดังนั้น …… (355)10 = (101100011)2
3 การเปลี่ยนทศนิยมเลขฐานสิบเป็นเลขฐานสอง การเปลี่ยนทศนิยมฐานสิบเป็นฐานสองนั้น ให้เอาทศนิยมฐานสิบตั้งแล้วเอา 2 คูณ ตัวทดที่ได้ (หน้าจุดทศนิยม) ซึ่งเป็นเลข 0 หรือ 1 คือ เลขฐานสอง การคูณจะคูณไปเรื่อยๆ จนผลลัพธ์มี ทศนิยมเป็น .0000
ตัวอย่างที่ 8 จงเปลี่ยน (0.5625)10 เป็นเลขฐานสอง
วิธีทำ
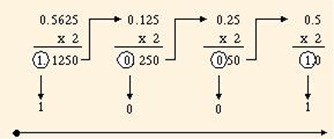
คำตอบ….. (0.5625)10 = (0.1001)2
ตรวจสอบคำตอบ…..
(0.1001)2 = (1 2-1) + (0 2-2) + (0 2-3) + (1 2-4)
= 0.5 + 0.0625
= (0.5625)10
ตัวอย่างที่ 9 จงเปลี่ยน (0.65625)10 เป็นเลขฐานสอง วิธีทำ

คำตอบ….. (0.65625)10 = (0.10101)2
ตรวจสอบคำตอบ…..
(0.10101)2 = (1 2-1) + (0 2-2) + (1 2-3) + (0 2-4) + (1 2-5)
= 0.5 + 0.125 + 0.312
= (0.65625)10
ตัวอย่างที่ 10 จงเปลี่ยนเลข (45.8125)10 ให้เป็นเลขฐานสอง วิธีทำ
ทศนิยม…..

ทศนิยมอ่านได้ ….. 0.1101
ดังนั้น ….. (45.8125 )10 = (101101.1101)2

ไม่มีความคิดเห็น:
แสดงความคิดเห็น