การเขียนสมการจากตารางความจริง การเขียนสมการจากตารางความจริงสามารถเขียนได้ 2 แบบ คือ แบบผลบวกของผลคูณ หรือแบบมินเทอม (Sum of Product Forms or Minterm Forms) และแบบผลคูณของผลบวก หรือแบบแม็กเทอม (Product of Sum Forms or Maxterm Forms)
1.การเขียนสมการแบบผลบวกของผลคูณ
สมการแบบผลบวกของผลคูณ คือสมการที่ประกอบด้วยเทอมที่ตัวแปรในเทอมนั้นแอนด์กัน โดยมีหลักการดังนี้ ถ้าตัวแปรอินพุตในแถวนั้นเป็นลอจิก “1” ให้เขียนตัวแปรนั้นใน รูปปกติ แต่ถ้าตัวแปรอินพุตในแถวนั้นเป็นลอจิก “0” ก็ให้เขียนตัวแปรนั้นในรูปของคอมพลีเมนต์ ดังแสดงในตารางที่ 9.1 และ 9.2 ในการเขียนสมการแบบผลบวกของผลคูณก็คือการนำเทอม ที่แอนด์กันในแถวที่เอาต์พุตมีค่าเป็นลอจิก “1” มาออร์กันดังตารางที่ 1
2. การเขียนสมการแบบผลคูณของผลบวก
สมการแบบผลคูณของผลบวก คือสมการที่ประกอบด้วยเทอมที่ตัวแปรในเทอมนั้นออร์กัน โดยมีหลักการดังนี้ ถ้าตัวแปรอินพุตในแถวนั้นเป็นลอจิก “0” ให้เขียนตัวแปรนั้นในรูปปกติ แต่ถ้าตัวแปรอินพุตในแถวนั้นเป็นลอจิก “1” ให้เขียนตัวแปรนั้นในรูปของคอมพลีเมนต์ ดังแสดงใน ตารางที่ 9.1 และ 9.2 ในการเขียนสมการลอจิกแบบผลคูณของผลบวก คือการนำเทอมที่ออร์กันในแถวที่เอาต์พุตมีค่าเป็นลอจิก “0” มาแอนด์กันดังตารางที่ 2
ตารางที่ 1 ตารางแบบมินเทอมและแม๊กเทอมของตัวแปร 3 ตัว
ลำดับที่่
|
INPUT
|
มินเทอม
|
แม๊กเทอม
| ||
A
|
B
|
C
| |||
0
|
0
|
0
|
0
|  |  |
1
|
0
|
0
|
1
|  |  |
2
|
0
|
1
|
0
|  |  |
3
|
0
|
1
|
1
|  |  |
4
|
1
|
0
|
0
|  |  |
5
|
1
|
0
|
1
|  |  |
6
|
1
|
1
|
0
|  |  |
7
|
1
|
1
|
1
|  |  |
ตารางที่ 2 ตารางแบบมินเทอมและแม๊กเทอมของตัวแปร 4 ตัว
| ลำดับที่ | อินพุต | มินเทอม | แม๊กเทอม | |||
| A | B | C | D | |||
| 0 | 0 | 0 | 0 | 0 |  |  |
| 1 | 0 | 0 | 0 | 1 |  |  |
| 2 | 0 | 0 | 1 | 0 |  |  |
| 3 | 0 | 0 | 1 | 1 |  |  |
| 4 | 0 | 1 | 0 | 0 |  |  |
| 5 | 0 | 1 | 0 | 1 |  |  |
| 6 | 0 | 1 | 1 | 0 |  |  |
| 7 | 0 | 1 | 1 | 1 |  |  |
| 8 | 1 | 0 | 0 | 0 |  |  |
| 9 | 1 | 0 | 0 | 1 |  |  |
| 10 | 1 | 0 | 1 | 0 |  |  |
| 11 | 1 | 0 | 1 | 1 |  |  |
| 12 | 1 | 1 | 0 | 0 |  |  |
| 13 | 1 | 1 | 0 | 1 |  |  |
| 14 | 1 | 1 | 1 | 0 |  |  |
| 15 | 1 | 1 | 1 | 1 |  |  |
การลดรูปสมการคณิตศาสตร์ทางลอจิก
การลดรูปสมการคณิตศาสตร์ทางลอจิก เป็นกระบวนการที่ทำให้สมการเหลือตัวแปรน้อยที่สุด เมื่อนำสมการที่ลดรูปนั้นไปประกอบเป็นวงจรก็จะได้วงจรที่ใช้จำนวนอุปกรณ์น้อย และสามารถทำงานได้ตามฟังก์ชั่นที่ต้องการ วิธีการที่นิยมใช้อยู่ในปัจจุบันมี 2 วิธีคือ การลดรูปสมการโดยใช้พีชคณิตบูลีนและการลดรูปสมการโดยใช้แผนผังคาร์โนห์
พีชคณิตบูลีน
พีชคณิตบูลีนเป็นการศึกษาการเปลี่ยนแปลงของตัวแปรในสองสภาวะ คือ 0 และ 1 ประกอบด้วยคุณสมบัติเบื้องต้นและทฤษฎี ดังต่อไปนี้
10.1.1 คุณสมบัติเบื้องต้นเกี่ยวกับการกระทำบนตัวคงที่
1) 0 × 0 = 0
2) 0 ×X = 0
3) 1 × 1 = 1
5) 0 + 1 = 1
6) 1 + 0 = 1
7)
= 
= 1 8)
= 
= 0 10.1.2 คุณสมบัติเบื้องต้นเกี่ยวกับการกระทำบนตัวแปร 1 ตัว
1) A + 0 = 0 + A = A
2) A + 1 = 1 + A = 1
3) A . 0 = 0 . A = 0
4) A . 1 = 1 . A = A
5) A + A = A
6) A . A = A
7) A +
= 1 8) A .
![clip_image106[1]](http://lh5.ggpht.com/-m_iH9busc9k/UFfbuSaMSQI/AAAAAAAABN4/RpdZaObdk7A/s1600-h/clip_image10612%25255B1%25255D.gif "clip_image106[1]"){kind=small}
= 0 9)
= A 10.1.3 คุณสมบัติเกี่ยวกับการกระทำบนตัวแปรมากกว่า 1 ตัว
1) A + B = B + A
2) A . B = B . A
3) (A + B) + C = A + (B + C) = A + B + C
4) (A . B) . C = A . (B . C) = A . B . C
5) A . B +A . C = A . (B + C)
6) (A + B) . (A + C) = A + (B . C)
7) A + A . B = A B + B.D = B
8) A . (A + B) = A B.(B+C) = B
9) A +
![clip_image106[2]](http://lh3.ggpht.com/-dKqoPV1nBFE/UFfbyMSnFdI/AAAAAAAABOY/WA1uRa0_yw4/s1600-h/clip_image10622.gif "clip_image106[2]"){kind=small}
.B = A + B ![clip_image106[3]](http://lh5.ggpht.com/-kp9neqWU_iI/UFfbzv6HxqI/AAAAAAAABOo/BIKJ7ivXaNU/s1600-h/clip_image10632.gif "clip_image106[3]"){kind=small}
+ A.B = ![clip_image106[4]](http://lh6.ggpht.com/-JM9uQUHq6CU/UFfb07yLYeI/AAAAAAAABO4/SlGmeEuG0VU/s1600-h/clip_image10642.gif "clip_image106[4]"){kind=small}
+B 10) A . (
![clip_image106[5]](http://lh3.ggpht.com/-Fmlk6SuNwe4/UFfb2HWjHSI/AAAAAAAABPI/AjZ-ksn0Bp0/s1600-h/clip_image10652.gif "clip_image106[5]"){kind=small}
+ B) = A . B ![clip_image106[6]](http://lh4.ggpht.com/-ZSzATlO056U/UFfb5PyYgFI/AAAAAAAABPY/l5hue0F3Ar0/s1600-h/clip_image10662.gif "clip_image106[6]"){kind=small}
. (A + B) = ![clip_image106[7]](http://lh6.ggpht.com/-iJBUVDtbq68/UFfb7O1qGQI/AAAAAAAABPo/dm0zo7uTR14/s1600-h/clip_image10672.gif "clip_image106[7]"){kind=small}
. B 11) A.B +
![clip_image106[8]](http://lh4.ggpht.com/-GmjhgYnZzqs/UFfb8TyPfhI/AAAAAAAABP4/DX3nu4h79xo/s1600-h/clip_image10682.gif "clip_image106[8]"){kind=small}
.C + B.C = A.B + ![clip_image106[9]](http://lh6.ggpht.com/-HF-DfNOJ0q4/UFfb9ZI59SI/AAAAAAAABQI/MAdyfgZopdg/s1600-h/clip_image10692.gif "clip_image106[9]"){kind=small}
.C 12) (A + B).(
![clip_image106[10]](http://lh3.ggpht.com/-EnUgmzUwIJI/UFfb-xvwn4I/AAAAAAAABQY/GiRS2UHr_l4/s1600-h/clip_image106104.gif "clip_image106[10]"){kind=small}
+ C).(B + C) = (A + B).(![clip_image106[11]](http://lh6.ggpht.com/-b59sX-7XZQY/UFfb_8fvo0I/AAAAAAAABQo/aSfjNSNFx3g/s1600-h/clip_image106114.gif "clip_image106[11]"){kind=small}
+ C) 10.2 การลดรูปสมการโดยใช้พีชคณิตบูลีน
การลดรูปสมการ โดยใช้พีชคณิตบูลีนเป็นกระบวนการในการเลือกใช้ทฤษฎี มาลดรูปสมการเพื่อทำให้เหลือตัวแปรในสมการน้อยที่สุด เมื่อนำสมการที่ลดรูปได้นั้นไปประกอบเป็นวงจร ก็จะได้ วงจรที่ใช้ลอจิกเกตน้อยที่สุด ที่ยังทำให้วงจรยังคงมีฟังก์ชั่นการทำงานเหมือนเดิม
ตัวอย่างที่ 10.1 จากวงจรที่กำหนดให้ จงเขียนสมการบูลีน ทำการลดรูปสมการให้เหลือตัวแปรน้อย ที่สุด แล้วเขียนวงจรลอจิกจากสมการที่ได้
 |
รูปที่ 10.1 วงจรลอจิกตัวอย่างที่ 10.1
วิธีทำ
สมการบูลีน Y = (A + B) . (B + C)
= (B + A) . (B + C)
= B+AC
จากสมการที่ได้นำมาเขียนวงจร
 |
รูปที่ 10.2 วงจรที่ได้จากการลดรูปสมการ
ตัวอย่างที่ 10.2 จากวงจรที่กำหนดให้ จงเขียนสมการบูลีน ทำการลดรูปให้เหลือตัวแปรน้อยที่สุด แล้วเขียนวงจรลอจิก จากสมการที่ได้ รูปที่ 10.3 วงจรลอจิกตัวอย่างที่ 10.2
วิธีทำ
สมการบูลีน Y = A + [(A + B) . BC]
= A + ABC + BBC A+ABC = A
= A + BC
จากสมการที่ได้นำมาเขียนวงจร
 |
รูปที่ 10.4 วงจรที่ได้จากการลดรูปสมการ
10.3 ทฤษฎี เดอ มอร์ แกน (De Morgan’s Theorem)
ทฤษฎี เดอ มอร์ แกน เป็นทฤษฎีที่ใช้ช่วยในการลดรูปสมการ ซึ่งประกอบด้วย
และ
เมื่อเขียนเป็นวงจรลอจิกจะได้เป็น
รูปที่ 10.5 วงจรลอจิกของสมการ
![clip_image119[1]](http://lh3.ggpht.com/-zxpJRRZxKpw/UFfcMbZeU7I/AAAAAAAABS4/Ws8AWw3cg-U/s1600-h/clip_image11914.gif "clip_image119[1]"){kind=small}
รูปที่ 10.6 วงจรลอจิกของสมการ
![clip_image121[1]](http://lh3.ggpht.com/-ASCv-kxLDA4/UFfcPT1Og9I/AAAAAAAABTY/mDUwRc7CdF4/s1600-h/clip_image12114.gif "clip_image121[1]"){kind=small}
เพื่อเป็นการพิสูจน์ว่าทฤษฎีของ เดอ มอร์ แกน กล่าวไว้ถูกต้อง สามารถพิสูจน์ได้โดยการสร้างตารางความจริงของสมการ ดังนี้
ตารางที่ 10.1 ตารางความจริงของ
และ 
| อินพุต | เอาต์พุต | ||||
| A | B | ![clip_image127[1]](http://lh6.ggpht.com/-4dNch-LMrMQ/UFfcTy6H0II/AAAAAAAABUI/DwWZfSXGeYc/s1600-h/clip_image12714.gif "clip_image127[1]"){kind=small} | ![clip_image106[12]](http://lh4.ggpht.com/-nL3W26IRegw/UFfcVJPkDoI/AAAAAAAABUY/ZLHZdi9gjbQ/s1600-h/clip_image106124.gif "clip_image106[12]"){kind=small} |  | ![clip_image129[1]](http://lh5.ggpht.com/-CVFy6rEn3Co/UFfcXRHksaI/AAAAAAAABU4/yOhiXf2t_BY/s1600-h/clip_image12914.gif "clip_image129[1]"){kind=small} |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
ตารางที่ 10.2 ตารางความจริงของ
และ 
| อินพุต | เอาต์พุต | ||||
| A | B |  | ![clip_image106[13]](http://lh4.ggpht.com/-YOW3l-DneSw/UFfcdl96hOI/AAAAAAAABV4/EcP7KUDm1aA/s1600-h/clip_image106134.gif "clip_image106[13]"){kind=small} | ![clip_image131[1]](http://lh4.ggpht.com/-v953eilEVKI/UFfce5qt-BI/AAAAAAAABWI/zVHFcZHhliI/s1600-h/clip_image13114.gif "clip_image131[1]"){kind=small} |  |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
จากตารางที่ 10.1 จะเห็นว่าค่าลอจิกที่เอาต์พุตของสมการ
![clip_image127[2]](http://lh6.ggpht.com/-6lsGA1npna4/UFfci0mvriI/AAAAAAAABWo/CeNmAgmWEH8/s1600-h/clip_image12724.gif "clip_image127[2]"){kind=small}
และ ![clip_image129[2]](http://lh6.ggpht.com/-oY5k8rSLCTo/UFfcj2277lI/AAAAAAAABW4/26AL6Q_4BXA/s1600-h/clip_image12924.gif "clip_image129[2]"){kind=small}
จะมีค่าเท่ากัน และจากตารางที่ 10.2 ค่าลอจิกที่เอาต์พุตของสมการ ![clip_image133[1]](http://lh3.ggpht.com/-2yGoDvaqIn8/UFfcml59qQI/AAAAAAAABXI/4gTs0Z_BYZU/s1600-h/clip_image13314.gif "clip_image133[1]"){kind=small}
และ ![clip_image135[1]](http://lh6.ggpht.com/-0Ceve9k8DOY/UFfcoPnSWXI/AAAAAAAABXY/KrBLMUH-kJk/s1600-h/clip_image13514.gif "clip_image135[1]"){kind=small}
ก็มีค่าเท่ากัน แสดงว่า ทฤษฎี เดอ มอร์ แกน ให้ค่าที่ถูกต้อง ตัวอย่างที่ 10.3 จากวงจรที่กำหนดให้ จงเขียนสมการที่จุด Y แล้วลดรูปสมการให้เหลือตัวแปรน้อย ที่สุด จากนั้นเขียนวงจรลอจิกจากสมการที่ลดรูปได้
 |
รูปที่ 10.7 วงจรลอจิกตัวอย่างที่ 10.3
วิธีทำ
สมการที่จุด Y =
=
=
=
=
=
จากสมการที่ได้นำมาเขียนวงจร
รูปที่ 10.8 วงจรที่ได้จากการลดรูปสมการตัวอย่างที่ 10.3 เมื่อเปลี่ยนรูปวงจรแล้ว
1 การลดรูปสมการโดยใช้แผนผังคาร์โนห์ (Karnaugh Map)
การลดรูปสมการโดยใช้แผนผังคาร์โนห์เป็นการลดรูปสมการอีกวิธีหนึ่ง ซึ่งจะทำให้ได้สมการที่สั้นลง โดยเขียนสมการให้อยู่ในรูปของผลบวกของผลคูณ หรืออยู่ในรูปผลคูณของผลบวกก็ได้
ลักษณะของแผนผังคาร์โนห์มีลักษณะเป็นตารางสี่เหลี่ยมที่มีจำนวนช่องของตารางแปรผันตามจำนวนของตัวแปร เช่นถ้ามีตัวแปร 2 ตัว ก็จะมีช่องของตาราง 4 ช่อง (22=4) ถ้ามีตัวแปร 3 ตัว ก็จะมี 8 ช่อง (23=8) หรือถ้ามีตัวแปร 4 ตัว ก็จะมี 16 ช่อง (24=16) การลดรูปสมการโดยใช้แผนผังคาร์โนห์สามารถลดรูปสมการที่มีตัวแปร 2,3,4,5 หรือ 6 ตัวแปร โดยทั่วไปมักจะใช้ลดรูปสมการที่มีตัวแปร ไม่เกิน 4 ตัว
1.1 ลักษณะของแผนผังคาร์โนห์
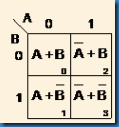
10.1.1.1 แผนผังคาร์โนห์ชนิด 2 ตัวแปรแผนผังคาร์โนห์ชนิด 2 ตัวแปร จะประกอบด้วยช่องซึ่งใช้สำหรับแทนเหตุการณ์ที่เกิดขึ้นกับตัวแปรจำนวน 4 ช่อง ดังรูปที่ 10.9
(ก) (ข)
(ค)
รูปที่ 10.9 แผนผังคาร์โนห์ชนิด 2 ตัวแปร
(ก) จำนวนช่องของตาราง
(ข) ค่าของตัวแปรแบบมินเทอม
(ค) ค่าของตัวแปรแบบแม๊กเทอม
1.2 แผนผังคาร์โนห์ชนิด 3 ตัวแปร
แผนผังคาร์โนห์ชนิด 3 ตัวแปรจะประกอบด้วยช่องซึ่งใช้สำหรับแทนเหตุการณ์ที่เกิดขึ้นกับตัวแปรจำนวน 8 ช่อง (23 = 8) ดังรูปที่ 10.10
(ก)
รูปที่ 10.10 (ก) (ข) แผนผังคาร์โนห์ ชนิด 3 ตัวแปร
1.3 แผนผังคาร์โนห์ชนิด 4 ตัวแปร
แผนผังคาร์โนห์ชนิด 4 ตัวแปรจะประกอบด้วยช่องซึ่งใช้สำหรับแทนเหตุการณ์ที่เกิดขึ้นกับตัวแปรจำนวน 16 ช่อง ดังรูปที่ 10.11
รูปที่ 10.11 แผนผังคาร์โนห์ชนิด 4 ตัวแปร
ตัวเลขที่กำกับด้านบนและด้านข้างของตัวแปร A,B หรือ C,D จะเป็นรหัส Gray code ซึ่งมีค่าเป็น 0 (00) , 1 (01) , 2 (11) และ 3 (10) ตามลำดับ ดังตารางที่ 10.3
ตารางที่ 10.3 รหัส Gray code ของเลขไบนารี 2 หลัก
| Decimal | 0 | 1 | 2 | 3 |
| Binary code | 00 | 01 | 10 | 11 |
| Gray code | 00 | 01 | 11 | 10 |
1.3.1 ขั้นตอนการลดรูปสมการโดยใช้แผนผังคาร์โนห์
การลดรูปสมการโดยใช้แผนผังคาร์โนห์มีขั้นตอนดังต่อไปนี้
1.ในกรณีเป็นสมการมินเทอมให้ใส่ลอจิก “1” ลงในช่องของแผนผังคาร์โนห์ตามค่าของตัวแปรในแต่ละเทอมของสมการ
2.ในกรณีเป็นสมการแม๊กเทอมให้ใส่ลอจิก “0” ลงในช่องของแผนผังคาร์โนห์ตามค่าของตัวแปรในแต่ละเทอมของสมการ
3. จับคู่และวงรอบตัวแปรที่เป็นลอจิก “1” ที่อยู่ติดกันในกรณีที่พิจารณาแบบมินเทอม หรือวงรอบตัวแปรที่เป็นลอจิก “0” ที่อยู่ติดกัน ในกรณีที่พิจารณาแบบแม๊กเทอม โดยพิจารณาวงรอบตัวแปรที่อยู่ติดกันจำนวน 16,8,4,2,1 ตัวตามลำดับ หมายความว่าถ้าลอจิก “1” หรือลอจิก “0” อยู่ ติดกัน ถ้าอยู่ติดกัน 16 ตัว ก็ให้วง 16 ตัว ถ้าอยู่ติดกัน 8 ตัวก็ให้วง 8 ตัว ตามลำดับ และถ้าวงรอบได้ 8 ตัว ก็ไม่ควรวงรอบ 4 ตัว 2 ครั้ง เพราะจะทำให้สมการที่ได้จะไม่ใช่สมการที่เหลือตัวแปรน้อยที่สุด
4. ช่องที่ถูกวงรอบไปแล้ว สามารถนำไปจับคู่เพื่อวงรอบร่วมกับตัวอื่นได้อีก
5. เมื่อวงรอบได้แล้วให้พิจารณาว่าจะได้ตัวแปรอะไรสำหรับวงนั้น โดยถือหลักว่าตัวแปรที่เหลืออยู่ก็คือตัวแปรที่ไม่เปลี่ยนสภาวะลอจิกเลยในทุก ๆ ช่องภายในวงรอบนั้น แต่ถ้าตัวแปรมีการเปลี่ยนแปลงให้ตัดตัวแปรนั้นทิ้งไป ดังรูปที่ 10.13
รูปที่ 10.12 แสดงค่าตัวแปรในพื้นที่ของแผนผังคาร์โนห์
ตัวอย่างที่ 10.4 จงลดรูปฟังก์ชั่นต่อไปนี้โดยใช้แผนผังคาร์โนห์ ก) f(A,B) =
ข) f(A,B) =
ค) f(A,B) =
วิธีทำ ก) ใส่ลอจิก “1” ลงในช่องของตาราง K-map สำหรับแต่ละเทอมตามที่โจทย์กำหนดแล้วทำการวงรอบ ได้ดังนี้
รูปที่ 10.13 แผนผังคาร์โนห์ ตัวอย่างที่ 10.4 (ก)
f(A,B) =
![clip_image168[1]](http://lh4.ggpht.com/-Znlg1BktIe8/UFfdGuJ6PlI/AAAAAAAABcI/w-NJYGULfsM/s1600-h/clip_image16814.gif "clip_image168[1]"){kind=small}
=
![clip_image106[14]](http://lh5.ggpht.com/--8-QP5YVBUo/UFfdI1tyhyI/AAAAAAAABcY/UuhXZVx842w/s1600-h/clip_image106144.gif "clip_image106[14]"){kind=small}
ข) ใส่ลอจิก “1” ลงในช่องของแผนผังคาร์โนห์ สำหรับแต่ละเทอมตามที่โจทย์กำหนด
แล้วทำการวงรอบ ได้ดังนี้
รูปที่ 10.14 แผนผังคาร์โนห์ ตัวอย่างที่ 10.4 (ข)
f(A,B) = ![clip_image170[1]](http://lh5.ggpht.com/-yET0oCVK7g8/UFfdLwTeIAI/AAAAAAAABdA/HiMSYXmtXLY/clip_image1701_thumb1.gif?imgmax=800 "clip_image170[1]")
![clip_image170[1]](http://lh3.ggpht.com/-9R05TCLkTS0/UFfdLWOSIGI/AAAAAAAABc4/bCB2pNfGfpA/s1600-h/clip_image17014.gif "clip_image170[1]"){kind=small}
= 
ค) ใส่ลอจิก “0” ลงในช่องของแผนผังคาร์โนห์ สำหรับแต่ละเทอมตามที่โจทย์กำหนด 
รูปที่ 10.15 แผนผังคาร์โนห์ ตัวอย่างที่ 10.4 (ค)
f(A,B) =
![clip_image172[1]](http://lh4.ggpht.com/-9G5lhVraDZ4/UFfdQo4O5pI/AAAAAAAABdo/_BGuKaTO8Rc/s1600-h/clip_image17214.gif "clip_image172[1]"){kind=small}
= B
ตัวอย่างที่ 10.5 จงลดรูปฟังก์ชั่นต่อไปนี้โดยใช้แผนผังคาร์โนห์
f(A,B,C) =
วิธีทำ
ใส่ลอจิก “1” ลงในช่องของแผนผังคาร์โนห์ สำหรับแต่ละเทอมตามที่โจทย์กำหนด แล้วทำการ วงรอบ ได้ดังนี้
รูปที่ 10.16 แผนผังคาร์โนห์ ตัวอย่างที่ 10.5
f(A,B,C) =
![clip_image183[1]](http://lh6.ggpht.com/-lViir7Ka8ME/UFfdUV-FWFI/AAAAAAAABeY/8v4AH7SSlyY/s1600-h/clip_image18314.gif "clip_image183[1]"){kind=small}
=
ตัวอย่างที่ 10.6 จงลดรูปฟังก์ชั่นต่อไปนี้โดยใช้แผนผังคาร์โนห์
ก) f(A,B,C) = Sm(1,3,6,7)
ข) f(A,B,C) = pM(0,1,2,3,4)
วิธีทำ
ก) นำค่าตามที่โจทย์กำหนดมาใส่ลงในแผนผังคาร์โนห์แล้วทำการวงรอบได้ดังนี้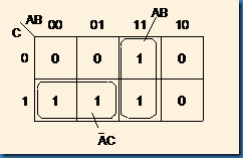
รูปที่ 10.17 แผนผังคาร์โนห์ ตัวอย่างที่ 10.6 (ก)
f(A,B,C) = Sm(1,3,6,7)
=
ข) นำค่าตามที่โจทย์กำหนดมาใส่ลงในแผนผังคาร์โนห์ แล้วทำการวงรอบได้ดังนี้
 |
รูปที่ 10.18 แผนผังคาร์โนห์ ตัวอย่างที่ 10.6 (ข)
f(A,B,C) = pM(0,1,2,3,4)
=
ตัวอย่างที่ 10.7 จงลดรูปฟังก์ชั่นต่อไปนี้โดยใช้แผนผังคาร์โนห์
f(A,B,C,D) =
ใส่ลอจิก “1” ลงในช่องของแผนผังคาร์โนห์ สำหรับแต่ละเทอมตามที่โจทย์กำหนด แล้วทำการวงรอบ ได้ดังนี้
รูปที่ 10.19 แผนผังคาร์โนห์ ตัวอย่างที่ 10.7
f(A,B,C,D) =
![clip_image198[1]](http://lh5.ggpht.com/-fcAcNZ_wWZs/UFfpVLrFccI/AAAAAAAABiQ/YiNKz1zR3QU/s1600-h/clip_image19814.gif "clip_image198[1]"){kind=small}
![clip_image200[1]](http://lh3.ggpht.com/-8bOD6HlEI5A/UFfpWT6CY4I/AAAAAAAABig/5eQnKBHqroE/s1600-h/clip_image20014.gif "clip_image200[1]"){kind=small}
=
ตัวอย่างที่ 10.8 จงลดรูปฟังก์ชั่นต่อไปนี้โดยใช้ แผนผังคาร์โนห์
f(A,B,C) = pM(1,3,5,7,8,10,12,14)
นำค่าตามที่โจทย์กำหนดมาใส่ลงในแผนผังคาร์โนห์ แล้วทำการวงรอบ ได้ดังนี้
รูปที่ 10.20 แผนผังคาร์โนห์ ตัวอย่างที่ 10.8
f(A,B,C) = pM(1,3,5,7,8,10,12,14)
= 
ตัวอย่างที่ 10.9 จงเขียนสมการและวงจรลอจิกจากตารางความจริงต่อไปนี้
ตารางที่ 10.4 ตารางความจริงตัวอย่างที่ 10.9
| อินพุต | เอาต์พุต | |||
| A | B | C | D | Y |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
นำค่าของตารางความจริงใส่ลงในตารางของแผนผังคาร์โนห์ แล้วทำการวงรอบได้ดังนี้
รูปที่ 10.21 แผนผังคาร์โนห์ ตัวอย่างที่ 10.9
จะได้สมการ Y = 
ได้วงจรลอจิก
รูปที่ 10.22 วงจรตัวอย่างที่10.9
1.3.2 สภาวะไม่สนใจ (Don’t care Condition) ในบางครั้งการออกแบบวงจรลอจิกอาจมีเงื่อนไขที่ไม่สนใจสภาวะที่เอาต์พุตเมื่ออินพุตมีค่าใดค่าหนึ่งดังตัวอย่างที่ 10.10
ตัวอย่างที่ 10.10 จงออกแบบวงจรให้ได้เอาต์พุตตามตารางความจริงต่อไปนี้
ตารางที่ 10.5 ตารางความจริงตัวอย่างที่ 10.10
| อินพุต | เอาต์พุต | |||
| A | B | C | D | Y |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
ค่าของอินพุตมีค่าตั้งแต่ 0000 ถึง 1001 เนื่องจากมีตัวแปรทั้งหมด 4 ตัว จะต้องใช้ แผนผัง คาร์โนห์ที่มี 16 ช่อง เมื่อนำค่าจากตารางความจริงมาใส่ลงใน แผนผังคาร์โนห์จะใส่ได้เพียง 10 ช่อง คือตั้งแต่ 0000 ถึง 1001 ช่องที่เหลือตั้งแต่ 1010 ถึง 1111 จะใส่เครื่องหมาย X หมายถึงเป็นสภาวะที่ไม่ สนใจ ในบางครั้งอาจสมมุติให้ช่องที่ใส่เครื่องหมาย X เป็น “1” หรือ “0” เพื่อช่วยในการวงรอบหรือจับคู่ร่วมกับช่องอื่น ๆ เพื่อให้การวงรอบได้จำนวนช่องมากที่สุด ดังนั้นเมื่อนำค่าที่ได้จากสมการมาใส่ลงในแผนผังคาร์โนห์แล้วทำการวงรอบได้ดังรูปที่ 10.23
จากตารางความจริงเมื่อพิจารณาในรูปของมินเทอมจะได้
Y = 
รูปที่ 10.23 แผนผังคาร์โนห์ ตัวอย่างที่ 10.10
จากตาราง K-map สมมุติให้ Y ในช่องที่อินพุตมีค่าเป็น 1010 ,1100 และ 1110 มีค่าเป็น “1” เพื่อช่วยในการวงรอบให้สามารถวงรอบได้จำนวน 8 ช่อง ส่วน X ในช่องที่อินพุตมีค่าเป็น 1011, 1101และ 1111 จะสมมุติให้เป็น “0” ไม่นำมาใช้ร่วมในการวงรอบ
ได้สมการ
Y = 
ตัวอย่างที่ 10.11 จงลดรูปฟังก์ชั่นต่อไปนี้โดยใช้ แผนผังคาร์โนห์
ก) f(A,B,C,D) = Sm(2,3,6,7,8,9) + d(10,11,12,13,14,15)
ข) f(A,B,C,D) = Sm(1,4,5,6,7,9) + d(12,13,14,15)
วิธีทำ
ก) นำค่าของแต่ละเทอมใส่ลงในตาราง K-map แล้วทำการวงรอบได้ดังนี้
รูปที่ 10.24 แผนผังคาร์โนห์ ตัวอย่างที่ 10.11 (ก)
ได้สมการ
f(A,B,C,D) = Sm(2,3,6,7,8,9) + d(10,11,12,13,14,15)
= 
ข) นำค่าของแต่ละเทอมใส่ลงในแผนผังคาร์โนห์ แล้วทำการวงรอบได้ดังนี้
รูปที่ 10.25 แผนผังคาร์โนห์ ตัวอย่างที่ 10.11 (ข)
ได้สมการ&nb
<3
ตอบลบ